The Chaocipher Clearing
House
Progress Report #27
4 August 2020
This Progress Report is a compilation of Chaocipher-related
information since Progress
Report #26 (February 2019).
Here's a brief listing of items:
- Chaocipher mentioned in Craig P. Bauer's book
"Unsolved!"
- Wolfram Function Repository has a Chaocipher function
- Chaocipher mentioned in Mike Barlow's "Computer Supplement
#5"
- Ken Hannigan's paper on John F. Byrne and his connection
to Wicklow, Ireland
- Rosetta Code: Chaocipher implemented in many programming
languages
- Roaming Zenith: An alternate way of displaying permuted
Chaocipher alphabets
- Chaocipher hypothesis re "no hits < 7" is finally
proven
- Call for someone solving "no hits < 7" in the
Crypto Forum
- Perl Weekly Challenge #25: Implement Chaocipher
- Off-the-wall link between Chaocipher and the Zodiac ciphers
- What is the reference here to Chaocipher?!
- Fascinating Chaocipher pt/ct challenge: find the starting
alphabets
- Musings regarding Chaocipher research
Chaocipher mentioned in Craig P. Bauer's book
"Unsolved!"
In Craig P. Bauer's excellent book "Unsolved! The History and
Mystery of the World's Greatest Ciphers from Ancient Egypt to Online
Secret Societies", we find, on pages 369-370, an
intriguing reference to Chaocipher.
Chapter 8, entitled "A Challenge Cipher", tells the story of Major
General Joseph O. Mauborgne (1881-1971). Mauborgne had an
illustrious army career, rising prominently in the Army Signal
Corps between the years 1914-1941. He served as the army's
twelfth chief signal officer from October 1937 until he reached the
mandatory retirement age in 1941.
In 1914, Mauborgne made his reputation when, as a young first
lieutenant, he achieved the first recorded solution of the Playfair
cipher, then used by the British as their field cipher. In
World
War I he independently invented the one-time pad.
In 1915, between these two events, Mauborgne, now a 1st Lieutenant,
submitted a challenge cipher message to the director of the Army Signal
School. The message was in a new system invented by
Mauborgne,
and he felt the
system was far superior to the Playfair or the M-94 cipher wheel
system. He suggested that members of the Signal
Corps should
be given the chance to solve it. Lou
Kruh, a
well-known collector of cryptological items and a prolific
cryptographic author, published Mauborgne's challenge cipher in the
American Cryptogram Association's "The
Cryptogram" and in Cryptologia, but no
solution was ever submitted by a solver.
When investigating the 1915 challenge cipher presented by Kruh, Bauer
wanted to see Mauborgne's original letter. Unfortunately, the
New
York Public Library could no longer find the original. In his
chapter 8, Bauer brings several examples of inaccuracies in Kruh's
articles, and opines that Kruh may have introduced errors into the
transcription of Mauborgne's cipher. One such inaccuracy
relates
to Lou Kruh's and Cipher Deavours's 1990 article in Cryptologia.
You can read the relevant portions of Chapter 8
describing Kruh's writing about Chaocipher. Bauer bases his
doubts about Kruh's accuracy on Jeff Calof's excellent paper in
Cryptologia entitled "Chaocipher
Exhibit 5: History, Analysis, and Solution of Cryptologia's 1990
Challenge".
Wolfram Function Repository has a Chaocipher function
The Wolfram Language is, according to its
Wikipedia page:
"
... is
a general multi-paradigm computational language developed by Wolfram
Research. It emphasizes symbolic computation, functional programming,
and rule-based programming and can employ arbitrary structures and
data. It is the programming language of the mathematical symbolic
computation program Mathematica."
The Wolfram Language syntax is overall similar to the M-expression of
1960s LISP, with support for infix operators and "function-notation"
function calls.
The Wolfram
Function Repository
is a public resource that hosts an expanding collection of contributed
standalone functions suitable for immediate use in any Wolfram Language
computation. Two of the standalone functions in the
repository
are the "ChaoCipher"
and "ChaoDecipher"
high-level functions for enciphering and deciphering Chaocipher
messages, respectively.
Chaocipher mentioned in Mike Barlow's "Computer Supplement #5"
The American Cryptogram Association (known as the ACA), one of the
oldest non-profit
organizations for hobbyist and puzzler cryptanalysts,
published a
computer-related publication named "The Computer
Supplement". First written and edited by the ACA member Mike
Barlow, the supplement ran from 1986 to 1997 and totaled 21 issues,
each filled with articles about computer programming code
(usually
BASIC) for use in solving ciphers presented in ACA issues.
Computer Supplement #5, published in January/February 1988,
presented an article entitled "Have you
tried the Chaocipher?"
Ken Hannigan's article "James Joyce, John Francis Byrne
and their Contemporaries: the Wicklow Connections"
In February 2012 I received an email from Ken Hannigan, a resident of
Dunganstown, West Wicklow, in Ireland. Ken had read my 2011
article on John Francis Byrne in Cryptologia, and this reawoke his long
interest in Byrne. As Ken wrote:
I
have been interested in J.F.Byrne for
many years, not because of any interest in ciphers, but originally as
part of research I was undertaking while a student in the 1970s on the
life of Francis Sheehy-Skeffington, a contemporary of
Byrne’s,
and more recently in connection with the history of my local parish of
Dunganstown, Co Wicklow. As you will be aware, J. F. Byrne wrote
extensively in his memoir, Silent Years, about the time he spent with
the Fogarty family in Carrigmore, Co. Wicklow. In 1993 and
1994
as part of a local history project in the parish, I co-operated with
Fr. Jim Murphy in taping a series of interviews with Michael Fogarty of
Carrigmore, the grandson of the man in whose house J.F. Byrne spent the
summers of his early life. I later published an article about
life in this area in the 1890s, based in part on Michael
Fogarty’s inherited memories and J.F. Byrne’s
memoir.
I am hoping now to write a little more for a local history society
about Michael Fogarty, who died in 2005, about his memories
or
previous generations, and what he had been told about visitors to
Carrigmore, including J. F. Byrne, Francis Sheehy Skeffington and James
Joyce (although I am almost certain that Michael Fogarty was mistaken
and that Joyce was never a visitor to Carrigmore).
This first email led to numerous fascinating and eye-opening
revelations over the years, as we both shared the information we had
about John F. Byrne. I must admit that carrying on such
interesting correspondences, with someone as erudite and enthusiastic
as Ken, has been a high point for me in my historical research into
John F. Byrne's life.
Ken's paper was first published locally in the Wicklow
Journal.
However, as is the way of excellent research articles, it was
picked up on by the prestigious Dublin James Joyce Journal, and the
editors invited him to submit a version of it to their
journal.
With Ken's permission, you can read his paper "James Joyce, John Francis Byrne and their
Contemporaries: the Wicklow Connections."
It is a scholarly, but a most readable, personal,
and
intimate account of John Francis Byrne's life in Ireland, and it
contains many references to Chaocipher.
September 2021
In May 2021, Ken Hannigan sent me an article entitled "The So-called Real Person who Lived at No. 7 Eccles St.: Extracts from 'Silent Years'".
The article provides historically valuable information about John
Francis Byrne. It was written by Elaine Byrne and published
in Wicklow Roots, The Wicklow County Genealogical Society Journal,
No. 9
(2004), published by Wicklow County Genealogical Society, Wicklow Town,
Co. Wicklow, Ireland. The introduction and the genealogical notes
on the Byrne Family were added by the editor of the journal, the late
Declan Byrne.
Rosetta Code: Chaocipher implemented in many programming
languages
The Rosetta
Code website defines itself as a "programming chrestomathy
site". The idea is to present solutions to the same
programming
task in as many different programming languages as possible.
This
helps demonstrate how languages are similar and different, and
aids a person with a grounding in one approach to a problem in learning
another. Rosetta Code currently (July 2020) has 1,060 tasks, 194 draft
tasks, and is aware of 791 languages.
One of its pages is dedicated to the Chaocipher
algorithm,
and solutions for coding the algorithm can be found in 26 different
programming languages, from Arc, C, and C# to Tailspin, Visual Basic
.NET, and zkl.
Roaming Zenith: An alternate way of displaying permuted
Chaocipher alphabets
In the original June 2010 document that revealed the Chaocipher system,
entitled "Chaocipher
Revealed: The Algorithm", the successive permuted left and
right alphabets of the sample enciphering were presented in
table form:
Left Alphabet
(ct)
Right Alphabet
(pt) CT
<- PT
HXUCZVAMDSLKPEFJRIGTWOBNYQ
PTLNBQDEOYSFAVZKGJRIHWXUMC
O W
ONYQHXUCZVAMDBSLKPEFJRIGTW
XUCPTLNBQDEOYMSFAVZKGJRIHW
A E
ADBSLKPEFJRIGMTWONYQHXUCZV
OYSFAVZKGJRIHMWXUCPTLNBQDE
H L
HUCZVADBSLKPEXFJRIGMTWONYQ
NBDEOYSFAVZKGQJRIHMWXUCPTL
Q L
QUCZVADBSLKPEHXFJRIGMTWONY
NBEOYSFAVZKGQDJRIHMWXUCPTL
H D
HFJRIGMTWONYQXUCZVADBSLKPE
JRHMWXUCPTLNBIEOYSFAVZKGQD
C O
CVADBSLKPEHFJZRIGMTWONYQXU
YSAVZKGQDJRHMFWXUCPTLNBIEO
N N
NQXUCVADBSLKPYEHFJZRIGMTWO
BIOYSAVZKGQDJERHMFWXUCPTLN
Y E
YHFJZRIGMTWONEQXUCVADBSLKP
RHFWXUCPTLNBIMOYSAVZKGQDJE
N I
NQXUCVADBSLKPEYHFJZRIGMTWO
MOSAVZKGQDJERYHFWXUCPTLNBI
X S
XCVADBSLKPEYHUFJZRIGMTWONQ
AVKGQDJERYHFWZXUCPTLNBIMOS
T B
TONQXCVADBSLKWPEYHUFJZRIGM
IMSAVKGQDJERYOHFWZXUCPTLNB
S E
SKWPEYHUFJZRILGMTONQXCVADB
RYHFWZXUCPTLNOBIMSAVKGQDJE
Z T
ZILGMTONQXCVARDBSKWPEYHUFJ
LNBIMSAVKGQDJOERYHFWZXUCPT
J T
JILGMTONQXCVAZRDBSKWPEYHUF
LNIMSAVKGQDJOBERYHFWZXUCPT
R E
RBSKWPEYHUFJIDLGMTONQXCVAZ
RYFWZXUCPTLNIHMSAVKGQDJOBE
R R
RSKWPEYHUFJIDBLGMTONQXCVAZ
YFZXUCPTLNIHMWSAVKGQDJOBER
H T
HFJIDBLGMTONQUXCVAZRSKWPEY
LNHMWSAVKGQDJIOBERYFZXUCPT
J H
JDBLGMTONQUXCIVAZRSKWPEYHF
MWAVKGQDJIOBESRYFZXUCPTLNH
B A
BGMTONQUXCIVALZRSKWPEYHFJD
VKQDJIOBESRYFGZXUCPTLNHMWA
Y N
YFJDBGMTONQUXHCIVALZRSKWPE
HMAVKQDJIOBESWRYFGZXUCPTLN
H W
HIVALZRSKWPEYCFJDBGMTONQUX
RYGZXUCPTLNHMFAVKQDJIOBESW
Q E
QXHIVALZRSKWPUEYCFJDBGMTON
SWYGZXUCPTLNHRMFAVKQDJIOBE
K L
KPUEYCFJDBGMTWONQXHIVALZRS
NHMFAVKQDJIOBRESWYGZXUCPTL
S L
SPUEYCFJDBGMTKWONQXHIVALZR
NHFAVKQDJIOBRMESWYGZXUCPTL
O S
OQXHIVALZRSPUNEYCFJDBGMTKW
WYZXUCPTLNHFAGVKQDJIOBRMES
U A
UEYCFJDBGMTKWNOQXHIVALZRSP
GVQDJIOBRMESWKYZXUCPTLNHFA
J I
JBGMTKWNOQXHIDVALZRSPUEYCF
OBMESWKYZXUCPRTLNHFAGVQDJI
Y D
We will call this presentation the "stationary zenith" permuting
method. This method reflects John F. Byrne's two-wheel physical model,
because at each enciphering step the alphabets rotate and shift up to
the stationary zenith position.
It turns out there is another, cryptographically identical method for
permuting the alphabets which we call the "roaming zenith" method.
The beauty of the "roaming zenith" permuting method is that
it
enables you to see, right before your eyes, the slow diffusion and
entropy of the Chaocipher alphabets.
For a clear description of both methods, see the page entitled "Two ways to
permute and display Chaocipher alphabets".
Chaocipher hypothesis re "no hits < 7" is proven
The first "Chaocipher
Progress Report",
published on this web site back in February 2009, highlighted an
intriguing characteristic in Exhibit #1 for in John F. Byrne's chapter
21 in "Silent Years". The observation was that identical
pt/ct
pairs (known as "hits") never occurred in Classic Chaocipher
at a
distance less than nine (9). This discovery fueled
almost
all of the Chaocipher research up
until the cipher system was revealed.
Chaocipher Progress Report #26, uploaded in February 2019,
announced the amazing fact that the
lower bound of hits occurring was not nine (9), but rather seven (7).
In other words, the phenomenon could be described as:
"Hits never occur at a distance
less than 7"
Additional research showed that, when exhaustively iterating through a
subset of possible encipherings, that seven (7) was indeed the
theoretical minimum. In other words, hits could never occur
at a
distance of 6, 5, 4, 3, 2, or 1.
In February 2019, a challenge was uploaded to the Tapatalk Crypto
Forum. The challenge was for readers to mathematically prove
that
seven (7) was indeed the theoretical minimum distance. At
the
time, no one took up the challenge.
I recently decided to "bite the bullet", and succeeded in proving the
assertion. The
proof can be read here.
Perl Weekly Challenge: Implement Chaocipher
The Perl
& Raku Weekly Challenge website
presents a weekly challenge to be solved in the Perl/Raku programming
language. Weekly challenge #25, posted on 8 September 2019,
stated the following challenge:
Create script to implement
Chaocipher. Please checkout wiki page for more information.
This challenge led to a flurry of activity trying to solve it.
Subsequent posts and links touched upon Chaocipher card
simulations, Pokemon sequences, and more.
Off-the-wall link between Chaocipher and the Zodiac ciphers
Here's a zany
monologue
that tries to connect James Joyce, John F. Byrne, and Chaocipher to the
Zodiac ciphers. Here is a quote from the end of the section:
Byrne
had included
a whole raft of enciphered text in his book along with the plaintext
equivalent – his aim was to allow someone the realistic
chance to
crack his cipher, after all. But, as a fail-safe, he encoded a final
section to which there was no plaintext provided. This would allow a
successful claimant to decipher the section and prove they had won the
prize.
That section was 17 letters long, one short of Zodiac’s
version.
I struggle to believe that this is just Zynch. In my opinion there is a
strong likelihood that Zodiac got inspiration for his final 18 letters
in the z408 from Byrne’s Chaocipher. If that is true then
those
18 letters almost certainly do have some meaning to decipher.
Beats me how anyone could consider such a connection, but it makes for
amusing reading.
What does this reference here to Chaocipher mean?
At the time of writing, I have not been able to figure out what this
link
has to say about Chaocipher, but you'll find it referring to Chaocipher
on page 3. If you can figure it out, drop me a line.
Fascinating Chaocipher pt/ct challenge: find the key
Reddit.com has many
communities within its borders, one of them being the /r/codes forum.
Here's how this community defines itself:
Hiding
data,
cracking codes, finding hidden messages. We welcome posts that aren't
as suitable for /r/crypto, such as basic cipher-cracking challenges and
discussions of simple data hiding.
On 10 July 2020, someone posted what he called "Challenges
no. 2 (classical ciphers)". In this post he offered
cryptographic challenges of different types. What interests
us is cipher #4:
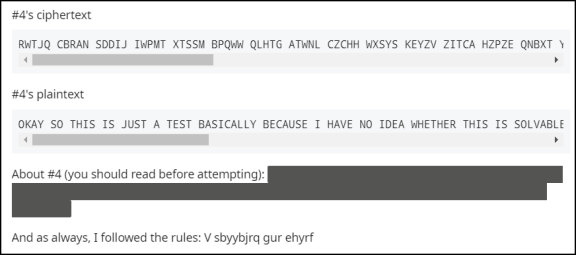
Clicking on the black area in "About #4" we see:
What we have here is a delightful challenge: given a Chaocipher
ciphertext and its corresponding plaintext, can you derive the starting
alphabets? This is precisely how the starting alphabets of
Exhibit #1 were found. For a technical explanation of how to
do
this, see George Lasry's on-line "A Methodology for the Cryptanalysis of
Classical Ciphers with Search Metaheuristics", section 8.3
("Related Work – Prior Cryptanalysis").
Here, for easy access, are the ciphertext and plaintext:
Ciphertext:
RWTJQ
CBRAN SDDIJ IWPMT XTSSM BPQWW QLHTG ATWNL CZCHH WXSYS KEYZV ZITCA HZPZE
QNBXT YQCBB VOBBI WTTWE GVCVE RLVUH XJXHT BEMPZ VONCX JPQRN BXTIK GBPQQ
ZHPWX XELXA LFPXY KZYDS FAWNP WEOHO EPDVQ FFOGE RHZSP XRJLK BIKIU APPRN
ILKSQ OTQPM GCAKK JJ
Plaintext:
OKAYS
OTHIS ISJUS TATES TBASI CALLY BECAU SEIHA VENOI DEAWH ETHER THISI SSOLV
ABLEG IVENT HEREL ATIVE LYLIT TLEAM OUNTO FCIPH ERTEX THERE AGAIN THERE
STHER EISPA DDING SOITI SATLE ASTAL ITTLE LONGE RINTH EHOPE THATT HISHE
LPSWI THDEC RYPTI ON
If anyone succeeds in determining the starting alphabets, please send
me a description of the method used and the starting alphabets, so I
can highlight your solution on this site.
Good luck on this real-world cryptanalytic challenge!
P.S. Use ROT-13
to decrypt the text "V
sbyybjrq gur ehyrf".
Musings regarding Chaocipher research
A reader of this website would be forgiven if he or she doubted the
long-term value of researching the Chaocipher cipher system.
After all, Chaocipher was never used as a real-life military
or
diplomatic cipher, and no historical documents were ever sent using the
system. So why invest time and energy in continued historical
and
cryptanalytic research into the system?
Besides the obvious answer of its being an intellectual challenge, I
believe Chaocipher research, and research of other crypto-systems, has
more far-reaching value. To date, this website has stimulated
both historical and cryptologic interest in other, sometimes unrelated,
areas. Here is a list of my thoughts and observations on this
topic:
- Even before the Chaocipher algorithm was discovered and
revealed,
amateur cryptanalysts were highly challenged to come up with a model
that would match observations. This was the best
cryptanalytic
exercise, sharpening our general understanding of techniques
for
tackling difficult cipher challenges.
- It has impacted historical research:
- A large corpus of historical correspondences was
collected
and published. This affords a history buff to read about
personages like William F. Friedman, Herbert O. Yardley, Parker Hitt, Rear
Admiral (ret.) Dundas Preble Tucker, and others.
- Chaocipher
research has led to fruitful fact sharing (e.g., see Ken
Hannigan's article above) that enrichen the wider historical picture.
- Craig
Bauer's research on Mauborgne's 1915 cipher (see above) benefited from
Jeff Calof's Chaocipher Exhibit #5 research.
- Chaocipher
afforded George Lasry, the indefatigable cryptanalytic researcher, to
add another cryptosystem to his impressive Ph.D thesis, "A Methodology
for the Cryptanalysis of Classical Ciphers with Search Metaheuristics"
(see Progress
Report #26).
Chaocipher enabled Lasry to test his thesis, for which Lasry
capitalized on the invaluable observation that Chaocipher's
ciphertext alphabet sequence does not add much security to the system.
His findings and observation will hopefully fuel
cryptanalytic
techniques in the future.
- Investigating
the "no hits < 7" phenomenon discussed above, we presented a
method
of proof that could be used when investigating other cipher systems
beyond Chaocipher.
- As
mentioned in my October 2011 paper "John F. Byrne's Chaocipher
Revealed" (pages * and *), the PURPLE cipher system and Chaocipher
shared several significant similarities. As I wrote then "Although
a moot point today, had Friedman observed similarities between
Chaocipher and Purple, he might have entertained the possibility that
Byrne had sold his idea to the Japanese. Regardless of what we know
today, documenting and studying Byrne’s Chaocipher within the
organization would have been a correct thing to do, notwithstanding the
heavy load on Friedman and his team ." Studying
seemingly unimportant or unrelated cryptosystems may help break others.
- The
Chaocipher concept has fired the imaginations of others to create
similar system (e.g., Aaron
Toponce's performing Chaocipher using playing cards) or to
write the Chaocipher algorithm in a large
number of different programming languages.
In summary, research in general, and Chaocipher research in particular,
can affect and impact other, unforeseen areas.
Copyright
(c) 2020 Moshe Rubin
Created: 4 August 2020
Modified: 6 September 2021
