Solution to "Battleships 3" Board with Incomplete Tallies

(from GAMES Magazine's "Brain Twisters: Volume 2", page 38, modified to give a unique solution)

Solution by: Shmuel Siegel

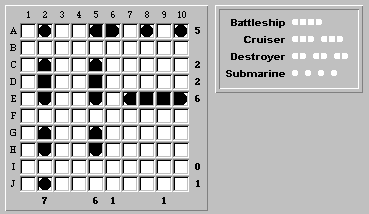
In GAMES Magazine's soft-covered "Brain Twisters from The World Puzzle Championships (volume 2)", you'll find two fascinating Battleship boards on pages 38 and 39. What is unique about them is that the reader is challenged to solve the boards, even though row and column tallies are missing! To quote GAMES Magazine, "Believe it or not, this is enough information to solve [the board]".

(NOTE: The original board, as presented in GAMES Magazine's Brain Twister Volume II, did not have a tally for row J. This resulted in multiple solutions. In the board presented here, we have added a tally of one for row J. This leads to the answer given in the magazine's solution section.)

Here is the initial board:

As you can see, there are row and column tallies missing. Amazingly, this is all the information we need to solve the board.

At first glance, there seems to be no obvious way to solve this board. The seemingly promising entry of trying to place the seven segments along column 2 produces too many possibilities. A brute-force solution is tedious and unsatisfactory.

The "Aha!" Insight

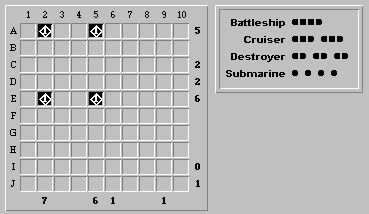
The "aha!" insight to solve this board can be seen by concentrating only on the rows A and E, and columns 2 and 5:



Here's Shmuel's brilliant observation:

  1. There are a total of 20 (twenty) ship segments hidden in this board (one battleships, two cruisers, etc.).

  2. Adding up the four tallies shown, we get 5+6+7+6=24 ship segments. This means that the two rows and two columns shown account for ALL of the ship segments to find (with four segments too many -- see next item).

  3. Since there are only 20 ship segments in this board, the intersection points (i.e. A2, A5, E2, E5) must be ship segments. The extra four segments (i.e. 24 rather than 20) are the result of counting the intersection points twice, once for the rows, and again for the columns.

  4. All the ship segments must reside on, and only on, these rows and columns.

Keeping the above points in mind, the board is easily solved. Because of item #3, we know that the intersection points are all ship segments:



Finalizing the board to fill in obvious water squares we get:



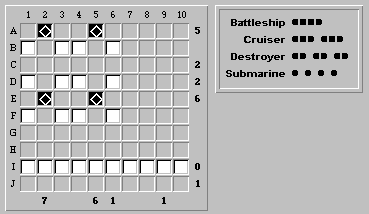
Look at row C. Because of item #4 above, we know that the two ship segments in this row must reside in columns 2 and 5. In other words, C2 and C5 must be ship segments. Similarly, row D's two ship segments must be found along columns 2 and 5. Therefore, we place ship segments at the intersections of rows C and D, and columns 2 and 5:



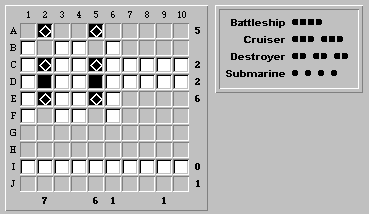
Filling in the remaining ship segments in row E gives us the battleship:



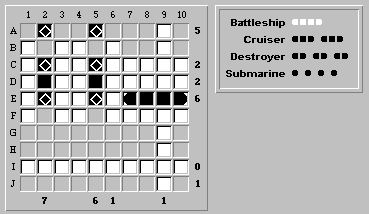
The two cruisers are obviously in columns 2 and 5:



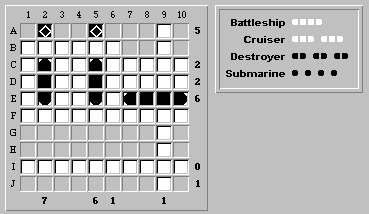
Filling in the remaining ship segments in column 2 gives:



Filling in column 5, followed by column 6, gives:



Since there are no more cruisers to place, A5-A6 is obviously a destroyer:



The only ships left to place are three submarines. (A,2) must be one of them. Since row A has a tally of 5, the remaining two submarines must be A8 and A10, which leads to the solution:



Return to Board Analyses and Solutions