Here is Wei-Hwa Huang's solution, in his own words:

NOTE: This does NOT imply in any way that Wei-Hwa supports, encourages, upholds or defends using the "board-uniqueness assumption" :-)

Here's an interesting application of the "uniqueness assumption":

Look at Hard 7x7 Board #4. (Unregistered)

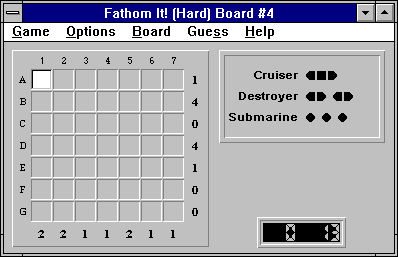
After you notice that rows C, F, and G are empty, you can immediately deduce that there must be a ship part in E1.

Why? Suppose there wasn't.

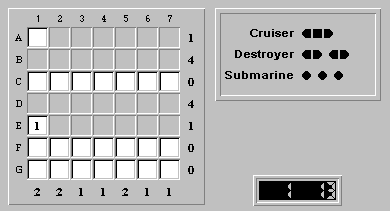
Then since you can switch rows B and D and rows A and E, then you get an alternate solution. Both solutions cannot be the same since the cruiser is only in one row.

But since we know that the solution is unique, there must be a ship part in E1.

This argument makes the puzzle MUCH easier than the other "hard" puzzles ...

Return to Board Analyses and Solutions