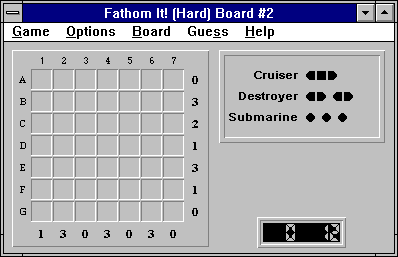
Solution to Fathom It! 7x7 Hard Board #2

Here's the initial board:

Finalizing any obvious water square (e.g. (A,1) as water) gives us the following:

Notice that columns 4 and 6 are symmetrical, both having a tally of three, and being surrounded by water squares.

We can deduce immediately that the solitary cruiser cannot be placed in either column 4 or 6. If it were, we could switch the columns around and have a different solution (because there is only one cruiser to place). This is not possible, because Fathom It! boards are guaranteed to have a single, unique solution.

Therefore, the cruiser must be placed in column 2:

Row E can be filled in with ship segments:

Looking at column 2, it is obvious that the cruiser that belongs there cannot extend to square (B,2). Therefore (B,2) is water, which means that all other unknown squares along row B are ship segments:

Filling in row C followed by row F gives the solution:

On 25 February 2005, Shmuel Siegel submitted analysis of this board that uses the symmetrical observation used above, but does not need the uniqueness principle:

"[The above solution] uses the uniqueness principle. The same logic can be utilized by using a symmetry argument which is right even if the solution was not unique.

"Consider your second diagram.  As you state, if a solution exists with the cruiser in column four, a solution exists with the cruiser in column six.  So choose six for convenience.  D6 is then a piece.  This closes off row D.  Then both columns two and four must have a vertical destroyer.  Whether the vertical destroyer of column two is on the top or the bottom, you are now faced with the daunting task of placing two submarines in a two by two square.  Hence the cruiser is in column two and the rest of your solution stands."

Return to Board Analyses and Solutions