Mountain Vista Software: Providers of Quality Battleship Puzzles

Solving a Digital Battleships Puzzle

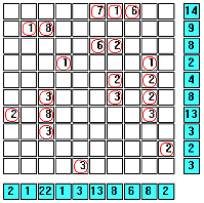
Here’s a simple Digital Battleships puzzle to solve:

The object is to locate a standard Battleships fleet (i.e., one battleship, two cruisers, etc.) on the grid. In this variation, the values on the right and bottom edges of the grid reveal the sum of the numbers in each of the ship segments that appear in each respective row or column.

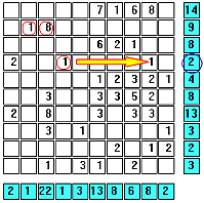
	The first step in solving any Digital Battleships puzzle is to erase all cells whose digit is greater than either the corresponding row or column tally. If any such cell were part of a ship, the tally would have been at least as large as the digit. For example, Row D has a row tally of two. Therefore, any cell in row D that has a digit greater than two cannot be part of a ship. See the next frame for what clearing away these cells in row D would look like.
	Let’s do the same for all rows and columns: erase all cells whose digit exceeds either its row or column tally. See the next frame for the result.
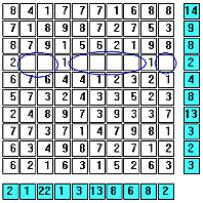
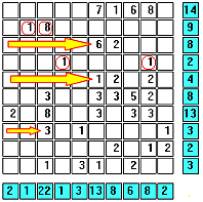
	This is certainly an improvement! The hidden fleet can only occupy the cells with digits in them. Now begins the fun. Column 2 has a tally of one. Since the circled cell, (B,2), has a value of one and is the only remaining cell in the column, it must be a ship segment. Since no ship can be adjacent to (B,2), the two circled cells in column 3 must be water.
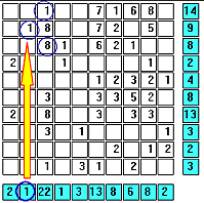
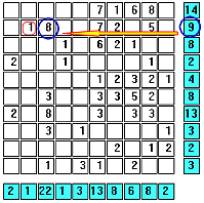
	Row B has a tally of nine. With cell (B,2) known to be a ship segment, we need to find a combination of cells along row B that would add up to eight. The digits 2, 5, and 7 cannot be combined to total eight. Therefore, cell (B,3), with a value of eight, must also be a ship segment. Marking (B,3) as a ship segment, erasing the remaining cells in row B, and erasing diagonally adjacent cells, we get …
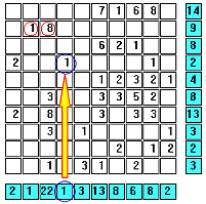
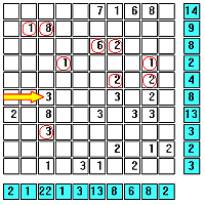
	Column 4 has only one remaining cell, so it must be a ship segment.
	Row D has a tally of two. Since we’ve already found a ship segment with a value of one, we only need to account for a value of one. Therefore, cell (D,9) must be a ship segment. Erasing unneeded cells and diagonally adjacent cells, we get the next frame.
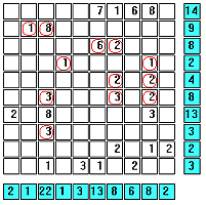
	It is obvious which cells are ship segments in rows C, E, and H (the row tallies can be satisfied in only one way). Remembering to remove diagonally adjacent cells gives us …
	All remaining cells in row F are ship segments.
	The rest of the solution is clear. The sequential steps are: · All remaining cells in row G are ship segments (which erases (A,9)). · Row A is fully accounted for. · Column 5 has one remaining cell. · Row I is determined.
	The puzzle is solved.

Click here to return to the Mountain Vista Software variations page